Disciplinary directions
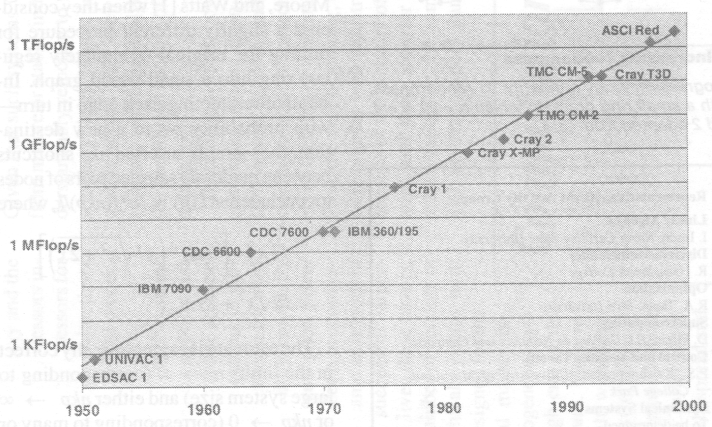
The post World War II yearshad been characterized by significant changes in the of sciences and industry brought about by what has come to be called the computer revolution, the mechanization of computation and information processing. There had been modest beginnings in earlier times (to which the names of Pascal, Leibniz, Jacquard, Babbage, Kelvin, Hollerith and others are attached in historical reconstructions), but it was not until the middle of the 20th century that computers and the many ramifications related to the theoretical tools needed for their applications became a field of its own, with research, funding and industrial development to back it up. Significant communities of scientists, engineers, technicians engaged in these developments appeared in developed countries throughout the world.
One of the earliest class of scientific problems solved by machines was that of computing the dynamics of mechanical and similar systems, those described with differential equations. Analog computers achieving this had been built since the 1930’s (Vannevar Bush at the MIT). ENIAC, the first significant digital computer– built at the University of Pennsylvania during the war years (Eckert, Mauchly, with a significant participation by von Neumann) was likewise intended for the solution of the differential equations, those describing the trajectory of projectiles above the Earth. And itis by no coincidence that it is the same class of problems that had led to the development of Calculus in the 17th century (Galileo, Huygens, Newton, Leibniz).
Two resulting communities — the analog and the digital — remained pretty much separated for a number of years, with some of the protagonists talking of a “war” between the two (which it was not). The digital side did gradually take over with the increasing power and decreasing cost of its hardware. Little analog computation was left by the middle 1970’s.
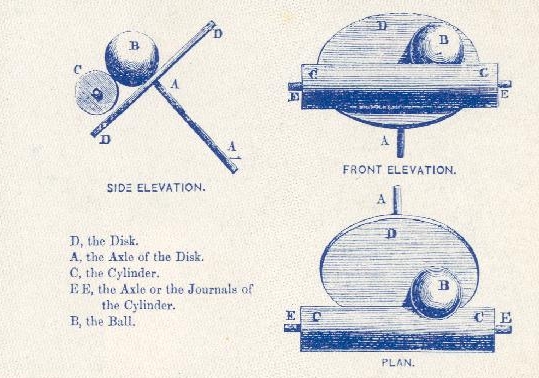
In the 1930’s, James Thomson’s ball and disk integrator (1876) was one of the first analog computing devices. It was used by Lord Kelvin, James Thomson’s brother, to describe the possibility of solving differential equations with machines. But It was not until several decades later (Vannevar Bush and colleagues at the MIT) that machines used to carry out actual calculations were to see the light.
An analog computer of the late 1950’s. Those machines were more powerful than digital computers for applications requiring modest accuracy, and IMACS (then still AICA) played an important role in the introduction of this computing tool in the industrial world, playing an important role in the beginnings of computer simulation in industrial and scientific development. E.g. they were essential to the US Space program of the 1960s, and held an important place in the study of the safety of the many nuclear power plants built in Europe in the post WW II years.

What is today at the center of IMACS’s disciplinary interests may be described in broad terms as the development of theoretical concepts and algorithmic tools that use computers (digital computers : analog computers have become practically obsolete) and mathematics, in the abstract as well as in the context of specific applications. They are “tools” in the sense that they will -at least in theory- be used by others, members of some “end use discipline” such as engineering and physics.
Those directions have changed and will by definition continue to change with time. New groups with particular interests appear, old ones become dormant (although some have shown remarkably stubborn resilience to do so irrespectively of what was happening in the outside world. We have in our midst nice examples and counter examples of the dynamics of what Thomas Kuhn called “Scientific Revolutions”).
The rise in power of electronic computers in the second half of the 20th century has been followed by a corresponding increase in the number of areas of research made possible by new tools in applied mathematics allowed by this new hardware. It is the development of those tools and related questions of mathematical modeling that have been – and still are – at the core of IMACS’s role in the applied sciences.